गतिविज्ञानम्
गणितविज्ञानम् | |
|---|---|
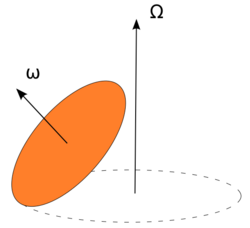 Euler महोदयस्य चक्र गणितविज्ञानम् |
गणितविज्ञानस्य (Dynamics) शाखायां यस्यां स्थिरवस्तुषु कार्यकतॄणां बलानां अध्ययनं क्रियते सा स्थितिविज्ञानमिति नाम्ना अभिधीयते । गत्वरेषु च कार्यशीलानां बलानां अध्ययनं यस्यां गणितविज्ञानशखायां क्रियते सा तु गतिविज्ञानमिति अभिवानं लभाते ।
(१) कस्यचित् वस्तुनः विरामावस्था, समरूप (uniform) गत्यवस्था वा येन बाह्यकारणे परिवर्त्यते, परिवर्त्यितुं वा प्रयत्नः क्रियते तद् बलम् (Force) इति कथ्यते । कल्प्यं यद् कश्चिद् गुरुपदार्थः पृथिव्यां स्थितः त्वया च तदुत्थापनार्थं प्रयलः क्रियते तर्हि त्वया तत्र बलं प्रयुज्ज्यते । यदि चेद् त्वदीयं बलं भुवः बलाधिकं भवेत् तर्हि त्वया पदार्थ उत्थाप्यते क्न्तु यदि चेद् त्वदीयं बलं पृथिव्याः बलान् न्युनं भवेत् तर्हि तद्वस्तु तत्रैव तिष्टति त्वदीयं बलं च अकिञ्चित्करं भवति ।
(२) बलस्य आघूर्णनम् (Movement of a force) कस्यचिद् अक्षस्य चतुदिक्षु कस्यचिद् बलस्य भ्रमणप्रयोजकः प्रभाव आघूर्णनमिति संज्ञां लभते । कस्यचिद् बलस्य आघूर्णनं तद्बलेन अक्षात् बलक्रियारेखापर्यन्तलम्बलम्बरूपान्तरालस्य गुणनफलेना तुल्यं भवति ।
कल्प्यं यद् कश्चिद् अक्षः ’अ’ इति बिन्दुतः अभिसरति तर्हि तस्य अक्षस्य चतुर्दिक्षु क्स्यचिद् ’ब्’ इति बालस्य आघूर्णनं ’ ब् x अ प ’ इत्यस्य तुल्यं भविष्यति । यत्र ’ अ प ’ इति अ इति बिन्दुतः ’ ब् ’ इत्यस्य क्रियारेखायाः लम्बरूपान्तरालम् अस्ति । यदि चेद् कस्यचिद् बलस्य क्रियारेखा कुतश्चिद् बिन्दुतः आभिसरति तर्हि, बिन्दोः चतुर्दिक्षु, तस्य बलस्य आघूर्णनम् शून्यं भवति ।
आघूर्णनसिद्धान्तः (Principle of Movement)
[सम्पादयतु]आघूर्णनसिद्धान्तम् अवगन्तुं एकेदृशी मीटरमापिका ग्राह्या यस्याः मध्ये शून्यचिन्हं स्यात् शुन्यस्य चोभयतः सेण्टीमीटरस्य चिह्नानि स्युः । मापिकामध्ये छिद्रमेकं कृत्वा तरैकं सूक्ष्मकीलकं निवेशनीयम् । कीलकं च एकस्मिन् आधारे संस्थाप्यम् दण्डश्च क्षैतिजः कार्यः । ततः मापिकायाः भुजयोर्द्वयोः तुल्यो विभिन्नसंहतिकौ वा माप्कौ सूत्रसहाय्येन प्रलम्बनीयौ । मापनीकायां तयोः स्थितिः तथा समञ्जनीयेयथा मापनिका क्षैतिजा भवेत् । विभिन्नसंहितिकाः मापकाः प्रलम्ब्य अन्यूनम् वारत्रयं प्रयोगाः करणीयाः परिणामाश्चेत्थं लेखनीयाः ।
यदि चेद् प्रयोगः अवधानपूर्वकं क्रियते तर्हि आलम्बरस्य दक्षिणपार्श्वस्र्थेन भारेण आलम्बात् तस्य अन्तरालस्य गुणनफलेन तुल्यं भविष्यति । अयमेव सिद्धान्त आघूर्णनसिद्धान्त इत्यमिधीयते ।
